2024年国考行测备考技巧干货：数量关系备考干货之奇偶特性的妙用

　　【导读】华图村官、三支一扶考试网同步未知发布：2024年国考行测备考技巧干货：数量关系备考干货之奇偶特性的妙用,详细信息请阅读下文!如有疑问请加【考试交流群汇总】 ，青海人事考试信息网更多资讯请关注青海华图微信公众号(htqh0258),第一时间获得第一消息。培训咨询电话：17797258271，备考QQ：732807461,微信号：17797258271

　　奇偶特性是较常见的一类整数特性，在解题过程中我们往往并不会应用奇偶特性直接解题，而是与代入排除结合使用，可以大大加快我们的解题速度。

　　一、奇偶特性及其推论：

　　首先我们要了解一下下面几个等式：

　　奇数±奇数=偶数;偶数±偶数=偶数;奇数±偶数=奇数。

　　通过观察以上加减法的等式，我们不难发现以下两个推论：

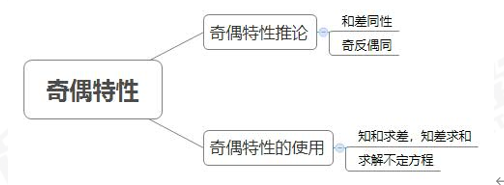
　　1.和差同性：两个数做和，如果结果是奇数，那么做差的结果也是奇数。如果做和结果是偶数，那么做差的结果也是偶数;

　　2.奇反偶同：如果两个数做和或者差的结果为奇数，那么这两个数一定是性质相反，即为一个奇数和一个偶数。如果两个数做和或者做差的结果为偶数，那么这两个数一定是同为奇数或同为偶数。

　　二、奇偶特性的应用：

　　1.知和求差，知差求和：当我们已知两个数的和，求两个数的差;或已知两个数的差，求两个数的和时，可以利用“和差同性”这个推论。结合代入排除，可以大大加快解题速度。

　　2.解不定方程：当遇到不定方程中的未知数系数出现偶数时，可以考虑使用“奇反偶同”这个推论来求解不定方程。

　　三、实战演练：

　　例1.四年级有4个班，不算甲班其余三个班的总人数是131人;不算丁班其余三个班的总人数是134人;乙、丙两班的总人数比甲、丁两班的总人数少1人，问这四个班共有多少人?

　　A. 177

　　B. 178

　　C. 264

　　D. 265

　　【思路点拨】本题正确答案为A选项。设甲、乙、丙、丁四个班人数分别为a、b、c、d，则所求为a+b+c+d的量。根据第二个条件可知(a+d)-(b+c)=1是一个奇数;我们把(a+d)和(b+c)分别看成两个整体，根据奇偶特性的推论“和差同性”可知(a+d)+(b+c)一定是一个奇数，因此我们所求的四个班级的人数和一定是奇数。可以排除B、C两个选项。剩余的两个选项我们只需要稍加分析即可，根据题干前半部分可知b+c+d=131，a+b+c=134，两个等式相加才等于265，大于四个班级人数的和。所以 排除D选项。因此，选择A选项。

　　例2.某儿童艺术培训中心有5名钢琴教师和6名拉丁舞教师，培训中心将所有的钢琴学员和拉丁舞学员共76人分别平均地分给各个老师带领，刚好能够分完，且每位老师所带的学生数量都是质数。后来由于学生人数减少，培训中心只保留了4名钢琴教师和3名拉丁舞教师，但每名教师所带的学生数量不变，那么目前培训中心还剩下学员多少人?

　　A. 36

　　B. 37

　　C. 39

　　D. 41

　　【思路点拨】本题正确答案为D选项。设每名钢琴、拉丁舞老师分别带领学员x、y人，由共76人，可列不定方程5x+6y=76。两个量的和为偶数，根据奇偶特性的推论“奇反偶同”可以推出5x、6y的奇偶性相同，而6y是6的倍数，一定是偶数，所以5x一定是偶数，故x为偶数。根据题干条件可知x也为质数，而2是唯一的偶质数，所以x=2，代入方程后可得y=11，即每名钢琴老师带2名学员，每名拉丁舞老师带11名学员。由所带学生数不变可得，剩余学员有4×2+3×11=41(人)。

　　好了，不知道小伙伴们是否学会了呢，奇偶特性在解题时对于我们提升做题速度往往有着巨大的作用，稍加练习就会熟练了哦!

（编辑：青海华图）