2024-08-22 15:15:39 国家公务员考试 https://www.huatu.com/ 文章来源:未知
青海人事考试信息更多资讯请关注青海华图微信公众号(htqh0258),第一时间获得第一消息。培训咨询电话:17797252905,备考QQ:732807461,微信号:17797252905

说起一元二次函数相信大家并不陌生,这让我们回忆起了校园时光,黑板上的抛物线就好像时光一样慢慢流逝。如今我们告别了校园,踏上了公务员的考试征途,再次遇见了熟悉又陌生的一元二次函数。在公务员考试中数量关系会涉及到此类考点,特别是在经济利润问题和几何问题中。而这两类题型是必考题型,大家要稳扎稳打拿高分,那么一元二次函数的应用就必须掌握牢固。
【学前启蒙】 :首先我们来回忆一下一元二次函数的基本知识,看看下面的函数图像,你还能想起些什么呢?
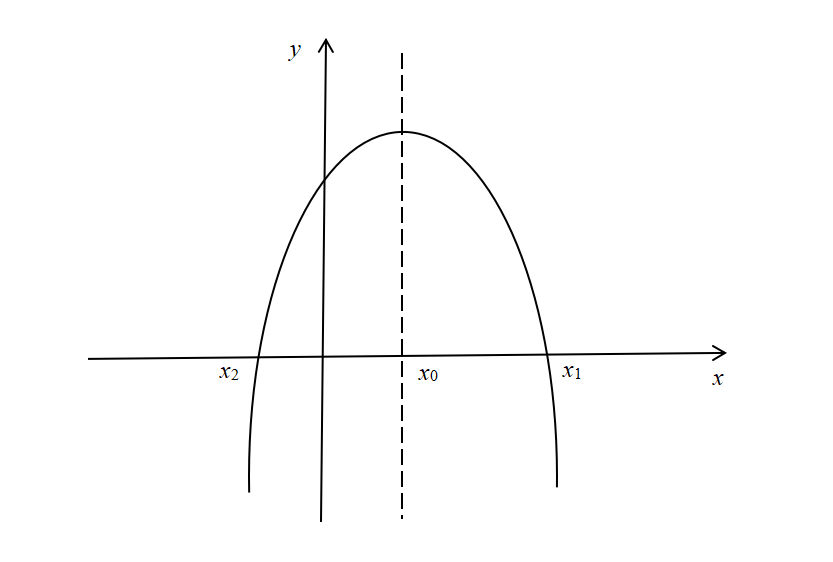
从图像上我们可以得出以下几个信息:
① 这是一个开口向下的抛物线,可以取得最大值。
② x= x0 是函数的对称轴 , 在 x = x 0 处函数取得最大值。
![]()
③ x1、x2分别是函数的两个根,且
利用以上基本信息,我们可以快速得到形如y=(x-m)(n-x)的最大值,方法如下:
① 分别令 x - m =0, n - x =0,则此函数的两个根分别是 m 、 n。
![]()
② 当时,函数取得最大值。
【课堂学习】 :接下来感受一下真题的考查形式,在学习中将知识内化于心。
1、经济利润问题统筹类:利润最大化
【例】 某商品的进货单价为80元,销售单价为100元,每天可售出120件。已知销售单价每降低1元,每天可多售出20件。若要实现该商品的销售利润最大化,则销售单价应降低的金额是 :
A.5元 B.6元
C.7元 D.8元
【答案】 C
【解析】第一步,本题考查经济利润问题 中的统筹类 。
![]()
第二步,设 销售单价 降低的金额为 x 元,即降了 x 个1元,则每件利润变为100-80- x =20- x , 销量变为120+20 x 。 根据总利润=单件利润 × 销量,则总利润为 (20- x ) (120+20 x ) =20(20- x ) ( 6+ x ) 。 分别令20- x =0,6+ x =0,得到此函数的两个根分别为20和-6,那么当时,此函数取得最大值 。 因此销售单价应降低7元。
因此,本题选择 C选项。
2、几何问题计算类:面积最大化
【 例】 村民陶某承包一块长方形种植地,他将地分割成如图所示的4个小长方形,在A、B、C、D四块长方形土地上分别种植西瓜、花生、地瓜、水稻。其中长方形A、B、C的周长分别是20米、24米、28米,那么长方形D的最大面积是:
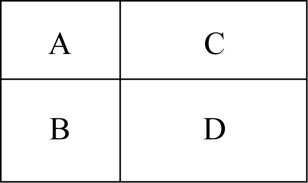
A.42平方米 B .49平方米
C.64平方米 D .81平方米
【答案】 C
【解析】 第一步,本题考查几何问题 中的 平面几何 计算 。
![]()
第二步,设A的长和宽分别为 x 米 、 y 米 ,由长方形A周长为20米,可得 x + y =10;由长方形B周长 为 24米,且长方形B与长方形A的长相同,可得B的长和宽分别为 x 米 、 y +2 米 ;由长方形C周长 为 28米,且长方形C与长方形A的宽相同,可得C的长和宽分别为 x +4 米 、 y 米 。那么长方形D的面积S=( x +4)( y +2)=( x +4)(10- x +2)=( x +4)(12- x ) , 分别令 x +4 =0 ,12- x =0,得到此函数的两个根分别是-4和12,那么当时,长方形D的面积最大, 此时S= ( 4+4)(12-4)= 64,故长方形D的最大面积为64平方米。
因此, 本题 选择C选项。
![]()
【课后总结】 由以上真题可以看出,一元二次函数类的考查主要集中在最大值的计算,由题干很容易得到形如y=(x-m)(n-x)的表达式。即使形式上有一些差别,我们也可以通过提取公因式等其他方式得到y=(x-m)(n-x) 的形式,然后令,此时函数可以取得最大值,由此便可以简化并快速解决问题。

贴心微信客服
上一篇:言语理解题型分析
下一篇:没有了