言语理解备考技巧：选言命题的分类

　　考试信息更多资讯请关注青海华图微信公众号(htqh0258),第一时间获得第一消息。培训咨询电话：17797252905，备考QQ：397590581,微信号：17797252905

　　在长期的一线教学当中，我们发现很多学生只了解选言命题中的一类，而对选言命题中的另一类搞不清楚。其实，选言命题不仅包含相容选言命题，而且还包含不相容选言命题，今天我们着重给各位考生分析一下这两种命题的区别。

　　想必不少考生也通过百度百科查询到了选言命题的概念，它是这样介绍的：“选言命题又称为析取命题，是反映事物的若干种情况或性质至少有一种存在的命题。根据选言支之间是否具有并存关系，选言命题可分为相容选言命题和不相容选言命题。选言命题由逻辑联结词“或者”连接支命题而成。其支命题称为选言支，通常用p、q表示。选言命题的逻辑形式可以写成：p或者q，符号为：p∨q(“p或者q”)。∨称为析取词。”通过以上的介绍，或许很多考生会有种似懂非懂的感觉。接下来我们就具体解释一下。

　　1.相容选言命题

　　首先我们来看相容选言命题。相容选言命题是表达两个(或以上)事物中,至少有一个真、也可以都真的判断。或者说表达了最多有一个假、不会都假的陈述句。既然可以都真，就说明两者并不是互相排斥的，在逻辑上称作“相容性”。直观上，相容选言命题是含有“或者......或者”等关联词，以及在语义上相同的陈述句。因为选言命题具有可选择其中某个或多个的特征，故亦称“析取”。如:

　　(例句1)甲精通英语，或者乙精通英语。

　　(例句2)甲和乙最少有一人精通英语。

　　(例句3)甲、乙两人，最多有一个人不精通英语。

　　这三个命题虽然表述方式不同，但语义是完全相同的。都是说甲乙二人中，至少有一个人是精通英语的，也可能两个人都精通英语。

　　我们以“甲精通英语，或者乙精通英语”为例。相容选言命题的符号形式表达为: pVq

　　读作:p或q。上述语句可表达为:甲精通V乙精通。甚至可简化为:甲V乙。

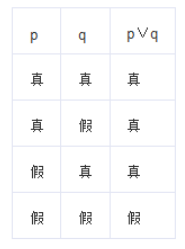
　　相容选言命题所反映事物的若干种情况或性质是可以并存的。例如：“小李会英语或者法语。”可以理解为小李可能既“会英语”又“会法语”，二者可以兼容，也就是同时存在。 相容选言命题的真值表可以表示如下：

　　下面通过一道真题来感知一下相容选言命题的运用：

　　【例1】某产品滞销或者是因为质量不好，或者是因为价格太高，或者是因为广告促销没有做好;经分析该产品质量很好。

　　那么：

　　A. 该产品滞销是因为价格太高

　　B. 该产品滞销是因为广告促销没有做好

　　C. 该产品滞销或者是因为价格太高，或者是因为广告促销没有做好

　　D. 该产品滞销既不是因为价格太高，也不是因为广告促销没有做好

　　【答案】C

　　【解题思路】

　　第一步，确定题型。

　　根据题干关联词“或者……或者……”，确定为翻译推理。

　　第二步，翻译题干。

　　①质量不好或价格高或广告促销没做好;

　　②质量好。

　　第三步，进行推理。

　　②否定了①的一支，依据“否定肯定式”的推理规则，可得③价格高或广告促销没做好;

　　A项，该项中的“价格高”只是③的一种可能性，不必然成立，排除;

　　B项，该项中的“广告促销没做好”只是③的一种可能性，不必然成立，排除;

　　C项，该项可翻译为“价格高或广告促销没做好”，与③完全一致，可以推出;

　　D项，该项可翻译为“-价格高且-广告促销没做好”，与③矛盾，排除。

　　因此，选择C选项。

　　2.不相容选言命题

　　而不相容选言命题又称为强析取命题，是反映事物的若干种情况或性质中有且只有一种情况存在的命题。如：

　　(例句4)小张和小王同时考一个岗位且只招一个人，要么小张考上了，要么小王考上了。

　　通过以上的例子，我们可以看出不相容选言命题所陈述的事物的若干可能情况是不能并存的。从例3可以得出：小张考上了，那么小王就不可能考上，两者不可能同时考上。

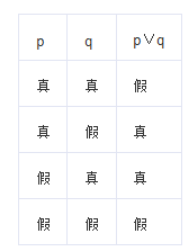
　　在逻辑结构上，不相容选言命题经常由逻辑关联词“要么，要么”连接支命题而成。这样，不相容选言命题的逻辑形式可以写成：要么p，要么q。 不相容选言命题的真值表可以表示如下：

　　下面再看一道关于不相容选言命题的例题：

　　【例2】某公司要从赵、钱、孙、李、周、吴等6位职员中挑选两人出国洽谈项目，在挑选时注意到了以下情况：(1)吴与钱不能同去;(2)只有孙去时，钱才能去;(3)若李去，则周也去;(4)要么赵去，要么李去;(5)如果钱不去，则赵也不能去;(6)由于某种原因，孙不能去。据此，可以推出：

　　A. 赵、周两人去

　　B. 李、吴两人去

　　C. 李、周两人去

　　D. 钱、吴两人去

　　【答案】C

　　【解题思路】

　　第一步，确定题型。

　　根据题干关联词“只有……才……”，确定为翻译推理。

　　第二步，翻译题干。

　　①¬吴或¬钱

　　②钱→孙

　　③李→周

　　④要么赵，要么李

　　⑤¬钱→¬赵

　　⑥¬孙

　　第三步，进行推理。

　　⑥是对②的“否后”，根据“否后必否前”，得到“¬钱”，排除D项;

　　“¬钱”是对⑤的“肯前”，根据“肯前必肯后”，得到“¬赵”，排除A项;

　　由④“要么赵，要么李”，由“¬赵”，得到“李”，而“李”是对③的“肯前”，根据“肯前必肯后”，得到“周”。

　　因此，选择C选项。

（编辑：青海华图）