数量关系备考技巧：巧解工程问题的效率类

　　考试信息更多资讯请关注青海华图微信公众号(htqh0258),第一时间获得第一消息。培训咨询电话：17797252905，备考QQ：397590581,微信号：17797252905

　　生活中，完成一件事情，做完一项工程，修完一条路等等这类问题称为工程问题。工程问题在公考中属于高频题型，接下来，小编给大家展示近5年工程问题在国考中的题型题量。

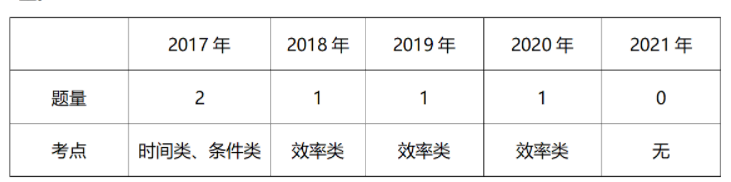
　　从统计表格可知，近5年，除了2021年，其余年份每年至少考一题，以效率类为主，工程问题在国考中的位置非常重要。接下来，小编通过3道题目展示效率类这类题型如何操作。

　　【例1】某公司有员工100人从事某产品的生产。现在，公司决定从这些员工中分流一些去生产新产品。分流后，继续从事老产品生产的员工平均每人每年创造产值在原有的基础上最多可增长1.2倍。若要保证老产品的年产值不减少，则最多能分流的人数是：

　　A.15人

　　B.16人

　　C.53人

　　D.54人

　　【答案】D

　　【解析】本题属于效率类。赋值每个人的效率是1，则100人一年创造产值100。假设分流人数是x,列方程得(100-x)×2.2=100，x≈54.5，取54，因此，选择D选项。

　　【例2】有甲、乙、丙三个工作组，已知乙组2天的工作量与甲、丙共同工作1天的工作量相同。A工程如由甲、乙组共同工作3天，再由乙、丙组共同工作7天，正好完成。如果三组共同完成，需要整7天。B工程如丙组单独完成正好需要10天，问如由甲、乙组共同完成，需要多少天?

　　A.不到6天

　　B.6天多

　　C .7天多

　　D.超过8天

　　【答案】C

　　【解析】本题属于效率类。设三者工作效率分别为甲、乙、丙，根据题意得2乙=甲+丙，(甲+乙)×3+(乙+丙)×7=(甲+乙+丙)×7;解得3乙=4甲，赋值甲的效率是3，乙的效率是4，则推出丙的效率是5。B的工作量=10×5=50，则甲乙合作时间是50÷7≈7...1，即7天多，因此，选择C 选项。

　　【例3】工程队接到一项工程，投入80台挖掘机。如连续施工30天，每天工作10小时，正好按期完成。但施工过程中遭遇大暴雨，有10天时间无法施工，工期还剩8天时，工程队增派70台挖掘机并加班施工。问工程队若想按期完成，平均每天需多工作多少个小时?

　　A.2.5

　　B.3

　　C.1.5

　　D.2

　　【答案】D

　　【解析】本题属于效率类。赋值每台挖掘机效率是1，则工作总量是80×30×10=24000，设平均每天多工作 t小时，列方程80×12×10+150×8×(10+t)=24000,解得t=2，因此，选择D选项。

　　怎么样，通过以上例题学习，小伙伴们，你学会了吗?让我们做一做下面的题目吧

　　【练习1】甲工程队与乙工程队的效率之比为4:5，一项工程由甲工程队单独做6天，再由乙工程队单独做8天，最后由甲、乙两个工程队合作4天刚好完成，如果这项工程由甲工程队或乙工程队单独完成，则甲工程队所需天数比乙工程队所需天数多多少天?

　　A.3

　　B.4

　　C.5

　　D.6

　　【答案】C

　　【练习2】某单位甲、乙、丙三人负责整理一项档案，他们工作5天完成了1/4，之后甲和乙因其他工作被调离，两天后才返回，期间丙继续整理档案。已知甲、乙、丙三人的工作效率之比为4∶3∶2，则完成这项工作共需要花费( )天。

　　A.20

　　B.21

　　C.22

　　D.23

　　【答案】C